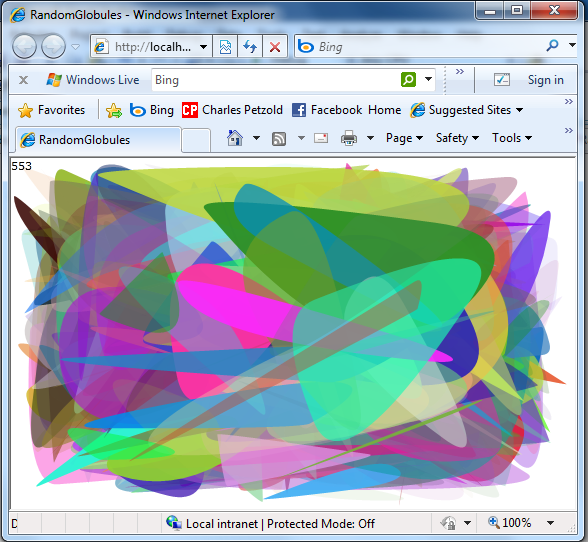
Random Globules This Time
November 2, 2009
New York, N.Y.
After I posted a blog entry on writing a random-rectangle program for Silverlight, I added a comment with links to Win16 and Win32 random-rectangle programs. It's really amazing to see how fast those old programs run on modern machines!
Can we persuade a WPF or Silverlight version to run as fast? I don't think so. Keep in mind that WPF and Silverlight implement retained-mode graphics systems where a composition layer is responsible for assembling all the visual objects into a composite video image. Retained-mode graphics is pretty much essential for the correct implementation of animation and transparency. But I am certain that the composition layer paces itself based on the video refresh rate.
The video refresh rate is typically 60Hz on modern displays, but it could be higher. The CompositionTarget.Rendering event fires at the same rate as the video refresh. WPF and Silverlight animations are also paced at this same rate. Of course you can always display multiple rectangles during each CompositionTarget.Rendering event, but these multiple rectangles will be displayed all together rather than sequentially, because the composite video image is only updated at that refresh rate. (I also attempted to generate random rectangles in a secondary worker thread, but didn't get any better results.)
So rather than make the program faster, I decided to take it in a different direction. This new program displays random irregular globules rather than rectangles:
Making these random figures turned out to be fairly easy, but the technique was not immediately obvious. To keep them simple, I decided that each globule would be a three-segment quadratic Bezier curve, defined by six points — alternating curve points and control points. To keep the circumference of the composite curve smooth, each pair of control points and the curve point between them should be colinear, that is, lie on the same line.
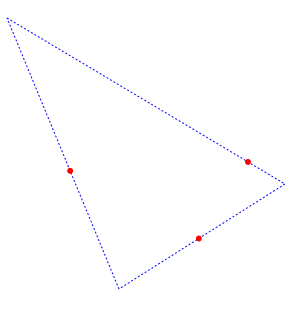
I started working on algorithms that began with the first random curve point, and sequentially generated random control points and curve points going around the figure, but I had to keep everything under constraints, and the logic soon got messy involving vectors and rotation angles. My conceptual breakthrough occurred when I realized I should start with the control points rather than the curve points. Once you see it, it's obvious: Begin by generating three random points within the size of the area where the object is to be drawn:

The three randomly generated control points form the vertices of a triangle. Because every pair of control points and the curve point between them must be colinear, the three curve points are simply random points on the lines connecting the control points:
Now we have six points to draw the three-segment quadratic Bezier:
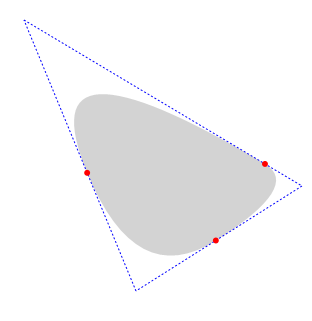
By itself it looks like this:

Here's the method in the program that generates the PathGeometry based on the dimensions of the drawing surface, which is actually the dimensions of the WritableBitmap:
PathGeometry GetRandomGlobule(int width, int height)
{
// Three control points
Point pt1 = new Point(rand.Next(width), rand.Next(height));
Point pt3 = new Point(rand.Next(width), rand.Next(height));
Point pt5 = new Point(rand.Next(width), rand.Next(height));
// Three end-points
Point pt0 = RandomBetweenPoint(pt5, pt1);
Point pt2 = RandomBetweenPoint(pt1, pt3);
Point pt4 = RandomBetweenPoint(pt3, pt5);
PathGeometry pathGeometry = new PathGeometry();
PathFigure pathFigure = new PathFigure()
{
StartPoint = pt0,
IsClosed = true
};
pathGeometry.Figures.Add(pathFigure);
PolyQuadraticBezierSegment polyQuadBezierSegment = new PolyQuadraticBezierSegment();
polyQuadBezierSegment.Points.Add(pt1);
polyQuadBezierSegment.Points.Add(pt2);
polyQuadBezierSegment.Points.Add(pt3);
polyQuadBezierSegment.Points.Add(pt4);
polyQuadBezierSegment.Points.Add(pt5);
polyQuadBezierSegment.Points.Add(pt0);
pathFigure.Segments.Add(polyQuadBezierSegment);
return pathGeometry;
}
Point RandomBetweenPoint(Point pt1, Point pt2)
{
double t = rand.NextDouble();
return new Point(pt1.X * (1 - t) + pt2.X * t,
pt1.Y * (1 - t) + pt2.Y * t);
}
Here's the downloadable RandomGlobule project.