Charles Petzold

I don't often identify with characters in novels, movies, or television programs, but when I do, it's probably not who you'd expect. Recently I've found myself feeling some affinity with Sally Draper on Mad Men. It might seem odd for me to "identify" with an 8-year old girl, but when you consider that the year is 1963, it makes a little more sense: Sally Draper is approximately my age. In recent episodes I've become more interested in how Sally views the world of 1963, and more importantly, how the 1963 world views her.

Some younger fans of Mad Men may have been surprised when Sally Draper wasn't allowed to attend her grandfather's funeral, particularly considering how close they had become in the weeks before he suddenly died. It's even possible Sally didn't know that the funeral was taking place, or even that there was such a thing as a funeral. I suspect this was a common practice with children in that era. When I was six weeks shy of my 8th birthday, I didn't attend my father's funeral, and I'm pretty sure I wasn't given any choice in the matter, or even that I knew that it was happening.

As far as I've been able to determine, Mad Men is impeccably researched. Whenever something has appeared in the program that I've questioned, I've later discovered that they got it right. (For example, Jackie Kennedy's famous TV tour of the White House really was broadcast on Valentine's Day.)

But in last Sunday's episode, Don and Betty Draper are having a little talk in a classroom with Sally's teacher, and I was startled to see on the blackboard several rather gory exercises in long division — but not the way I learned long division!

The long division shown on the blackboard in Mad Men looked like this (except adorned with several downward pointing arrows):

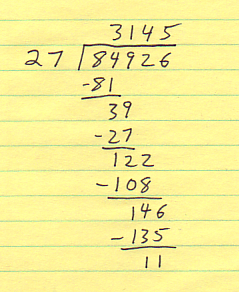
This is called — I didn't know these terms until I did a little Internet research this week — the Column Division method. For each digit of the quotient you need to mentally find the largest number that when multiplied by the divisor won't exceed the remaining dividend.

In a public school in New Jersey I learned a technique of long division called the Partial Quotients method:

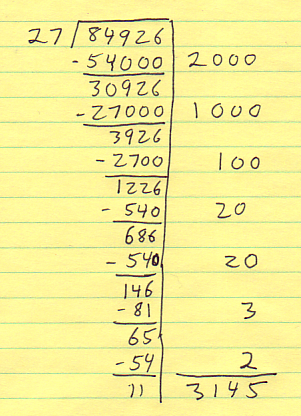
Each of the numbers to the right of the vertical line is multiplied by the divisor and then subtracted from the remaining dividend. The advantage of Partial Quotients is that you don't have to nail each digit exactly. You can build up to it because you're accumulating a list of numbers that sum to the total quotient.

I remember my mother attending a parent-teacher evening where my teacher demonstrated this method to the parents as the latest and greatest way for kids to do long division. I know this because she later asked me about it, and then showed me the way she learned long division, and since that time I guess I assumed that the method I learned was ubiquitous in the early 60s — at least in schools in the northeast.

But I'm probably wrong about that. I suspect that different schools and different teachers taught long division differently, and it appears as if the Partial Quotients method is still sometimes taught, although I hope that Column Division is then introduced as an alternative, and Short Division as an option when the divisor is small. (Obviously, the more of the division process that is moved to the brain, the smarter the student becomes.)

Still, I think Matthew Weiner missed an opportunity here: A blackboard full of exercises in Partial Quotient long division might have seemed more unusual and "exotic" — and emphasized once again just how long ago 1963 really was.